CS速成课笔记
前言首先是大致介绍笔记组成,来源,参考以及建议。
内容源于【计算机科学速成课】- Crash Course Computer Science ,是学习时做的一些简单笔记,从别的大佬的笔记里扒了不少内容和图片,仅用于自己学习复习时使用。加了一些自己帮助学习的例子
私货。原字幕我看文件大小估计至少12w个字(因为是双语字幕而且经常出现重复行,源文件938k直接砍半抹零头保守估计400k,然后假定文件使用UTF-8编码,则一个汉字3b,那么20kb就包含6000多个汉字,那这400k就保守估计出12w的汉字了)那我这笔记还算精炼的Σ(っ °Д °;)っ
笔记组成大致如下
1-9章:计算机基本组成 - 从开关到逻辑门到CPU
10-16章:编程语言 - 编程方式语言发展,处理数据方法的发展
17-23章:操作系统与文件系统 - 怎样管理计算机与相关文件
24-25章:促进计算机发展的历史 - 战争与商业化对计算机的发展促进
26-27章:计算机图形界面 - 计算机与人交互方式的简化
28-30章:互联网组成 - 计算机数据交互方式的发展
31-33章:计算机安全 - 网络数据安全怎样受到挑战与保护手法
34-40章:计算机拓展应用 - 让计算机利用自身优势做的从与人类相似到超越人类
1-27章: 计算机发展到从专注硬件到软件,专注于将计算机贴近人类
28-40章:计算机网络与AI教育,专注于将计算机超越人类
建议学习时如果像我一样觉得看视频太拖沓(但是视频补充的例子确实很关键)可以参考他人笔记以及视频字幕。
偏概括的笔记,作者记到压缩那一章附近就没了,CrashCourse_CS_notes (P1-P5) - Syddd的文章
相对完整的笔记,但是作者中间互联网到加密那一块没有做笔记。计算机科学速成课笔记 - 问夏的文章
计算机的基本元件-开关
前一章感觉只是介绍历史的草草看过觉得没有特别需要注意的就没特意去记笔记
计算机是由各种电路组合而成的,而电路由电源,用电器(负载),中间环节(导线,开关)组成。以下是开关的演变,从继电器到真空管到晶体管。
继电器
早起的电路开关继电器是用电控制的机械开关,它连接着一个线圈,当线圈通电时会产生感应磁场吸引上方机械臂从而闭合电路(联通线路得到高电平)。但是金属机械臂是有质量的,无法快速开关而且反复移动会很容易产生损耗。
真空管
单项流通电流 - 二极管
热电子管把两个电极放在一个气密的真空玻璃灯泡中。其中一个电极A可以加热以发射电子(热电子发射Thermioic emission),另一个电极B则会吸引电子来形成电流。只有当电极B带正电时才能吸引电子,否则电子无法从电极A跨越真空区域。这种电流只能单向流动的电子部件就是二极管(二极管通常让电流从阴极流向阳极,吸引电子的被称为阳极,发送电子的被称为阴极)。

可控制电流开闭 - 三极管
而之后又在两个电极间加入了第三个控制电极,向控制电极施加正电荷会允许流动,反之则阻止电子流动。因此通过控制线路开闭实现了继电器的功能的就是三极真空管。因为真空管内没有会动的组件,意味着更少的磨损,但是也相对比较脆弱而且会像灯泡一样烧坏,体积也比较大。

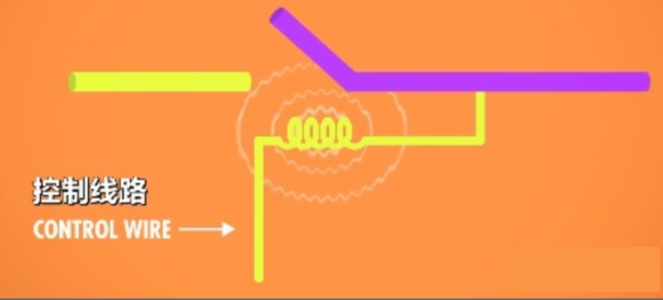
晶体管
晶体管也是一个用于控制电路闭合断开的开关,晶体管有两个电极,这两个电极之间通过半导体材料隔开。半导体这种材料有时候导电,有时候不导电(常温下导电性位于导体与绝缘间,通过外界干扰改变导电性)。而控制线链接到一个”门“电极,通过改变门的电荷就可以改变半导体材料的导电性。控制了半导体导电性就可以控制电流是否流动了。
布尔逻辑和逻辑门
布尔逻辑
布尔逻辑把一些简单的逻辑思维数学化,而此处逻辑即判断事物真假或是非,布尔逻辑以代数的形式将真假区分为变量值true和false。
例:
- 所有人都会死(大前提,true)
- 苏格拉底是人(小前提,true)
- 所以,苏格拉底也是会死的(结论,true)
以上例子是亚里士多德提出的经典逻辑三段论,客观推导下结论必然为真,而布尔代数则是多个判断之间的逻辑关系演算,也被称为逻辑代数。即用布尔逻辑以布尔代数的形式运算多个判断之间的关系。
布尔代数
布尔代数不是算数运算,但仍有相应的规则与运算法则
- 布尔代数中,数值只能取
true和false或者0和1- 布尔代数中,变量可以进行
"或且非"三种逻辑操作- 布尔运算满足
交换律,结合律,吸收律,反演律
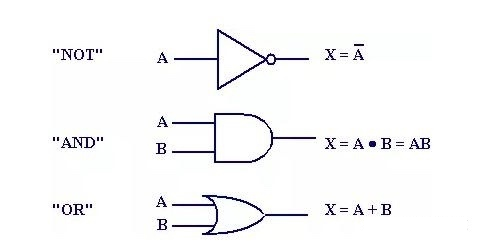
逻辑门
在计算机中布尔逻辑以开关接通状态为1(true),开关不通状态为0(false)。这样就可以用电路的开关模拟逻辑状态,组成逻辑电路。又因为组成的逻辑电路可以控制电流的流通堵塞与路径,又被称作逻辑门。
AND 与门
对应布尔代数且操作,设有两输入A,B其同时为TRUE时输出TRUE,否则都输出FALSE
| 输入A | 输入B | 输出 |
|---|---|---|
| T | F | F |
| F | T | F |
| T | T | T |
| F | F | F |
此处使用T代表True,F代表False,像这样列出所有情况的表也称为真值表
OR 或门
两输出其中一个为TRUE则输出TRUE,都不为TRUE则输出FALSE
| 输入A | 输入B | 输出 |
|---|---|---|
| T | F | T |
| F | T | T |
| T | T | T |
| F | F | F |
NOT 非门
非门只接受一个输入,且会将输入置反,即输入TRUE输出FALSE,输入FALSE输出TRUE
| 输入A | 输出 |
|---|---|
| T | F |
| F | T |
XOR 异或门
异或门是基于以上三种逻辑门构建的,其逻辑为接受两个输入,两输入相同则输出FALSE,输入不同则输出TRUE
真值表如下
| 输入A | 输入B | 输出 |
|---|---|---|
| T | F | T |
| F | T | T |
| F | F | F |
| T | T | F |
其中电路图如下,最好将真值表带入进行运算一遍,还可以试试用红石电路实现(因为红石电路不懂怎么优化结构,最后只实现一个全加器就没有接着做了)
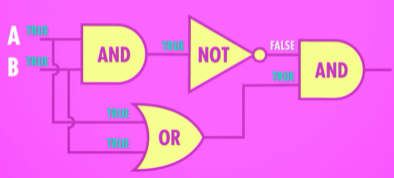
理解异或门组成后便可将其抽象,概括为与其它逻辑门一样直接用于运算即可,不必关心具体实现用了几根晶体管
二进制
二进制表示正负整数
二进制以01表示任何整数,简单说便是逢2进1。
例如
- 十进制8可以二进制表示为0000 1000(前方0补位,表示八位二进制)
- 十进制11可表示为二进制 0000 1011
例子中二进制以八位二进制数至多表示0到255,即0至$2^8 -1$平时常见的二进制数通常是32位类型。而能表示到最大255是因为此处忽略了符号,即此前二进制表示为无符号整数,如果需要表达负数数值范围会改为 -128至127(1000 0000 至 0111 1111)
而二进制也可以表示负数,二进制位数中最高位为符号位,其为1时则表示是负数。(即表示正数还是负数看人,也看下面的码制)
如
- 1000 1000 可表示为二进制 -8(八位二进制,有符号表示为-8,无符号则表示为136)
码制
计算机中的符号数有三种表示方法,即原码,反码和补码。三种表示方法均有符号位和数值位两部分,符号位都是0表示正,1表示负。数值位则三种表示方法都不同。原码…嗯…就是原码即符号位加上数值位真值的绝对值
例
- 0000 1001 原码 = +9(八位二进制原码表达范围为-127至127)
反码
- 正数:反码与原码完全相同
- 负数:符号位保持为1,数值位逐位取反(每位0→1,1→0)
将二进制每一位取反 (即用每一位都是1的二进制数去减操作数)
例
- +9 反码 = 0000 1001(与原码相同)
- -9 原码 = 1000 1001 → 反码 = 1111 0110(八位反码范围-127至127)
补码
- 正数补码 = 原码
- 负数补码 = 反码 + 1
注意计算机中数值都是以补码形式存储
其优势在于:
- 统一+0和-0的表示(补码中0000 0000唯一表示0)
- 简化减法运算(A - B = A + (-B)补码)
- 可多表示一个最小值(八位补码可表示-128)
例
- +9 补码 = 0000 1001(与原码相同)
- -9 反码 = 1111 0110 → 补码 = 1111 0111(八位补码范围-128至127)
此处补码能表示至-128 是因为 1000 0000 数学上表示为128,而原码反码在8位内存中无法表示, 又因为表示补码有限保证符号位不变,而1000 0000恰好保证补码表示为负数,与0000 0000表示一个就浪费了,刚好多表示一个数即-128
补码的补码又等于原码即 原码 取反 +1 取反 +1 = 原码
例:
1001 补码 = 0111 补码 → 1001
bit和byte
1位二进制为1bit,八位2进制则为1bytes
1bytes = 8bits
1Mb = 1024bytes
1Gb = 1024Mb
1Tb = 1024 Gb
二进制表示 浮点数
浮点数(如1.14514)等小数是程序中常用的数据类型,而现代计算机一般都以IEEE 754标准存储浮点数,在内存中存储的形式为:
| 数字符号位(数符) | 指数位(阶码) | 有效位数(尾数) |
|---|---|---|
| sign | exponent | fraction |
不同长度的浮点数指数位于小数位分配数量不同,其中常用浮点数分配位数表如下
| sign | exponent | fraction/significand | all | offset | |
|---|---|---|---|---|---|
| 32位单精度浮点数 | 1 | 8 | 23 | 32 | 127 |
| 64位单精度浮点数 | 1 | 11 | 52 | 64 | 1023 |
以下是浮点数转二进制的例子:
例如114.125(很想写514但是转成小数位数太多了)
先把整数部分和小数部分转换成二进制
整数部分除二求余得: 1110010
小数部分乘二取整得: 001
- 0.125 x 2 =》 0 0.25 x 2 => 0 0.5 x 2 => 1 1 ==> 001
合起来为1110010.001转换为二进制浮点数,即把小数点移动到整数位只有1,即为: 1.110010001 * 2^110 小数点左移6(二进制110)位.
二进制浮点数对应三部分的值
- 数字符号位: 浮点数为正数,此处为0
- 指数计算公式为: 指数位数+偏移量, 偏移量为(2^(e-1)-1);e为指数位数。此处指数位数为刚才左移的位数,此处为110,此处为32位单精度小数,偏移量为127,因此指数为: 110 + 01111111 = 10000100,尾数则为小数点后数:110010001
- 则最终结果为
01000010011001000100000000000000
二进制表示文字-Ascii码
用于表示文字(英文字母等)经常会使用的是Ascii码,由七位二进制组成的,默认只收录了128个字符,后128个是拓展Ascii码用于收容外来语字母,图形符号和数学符号
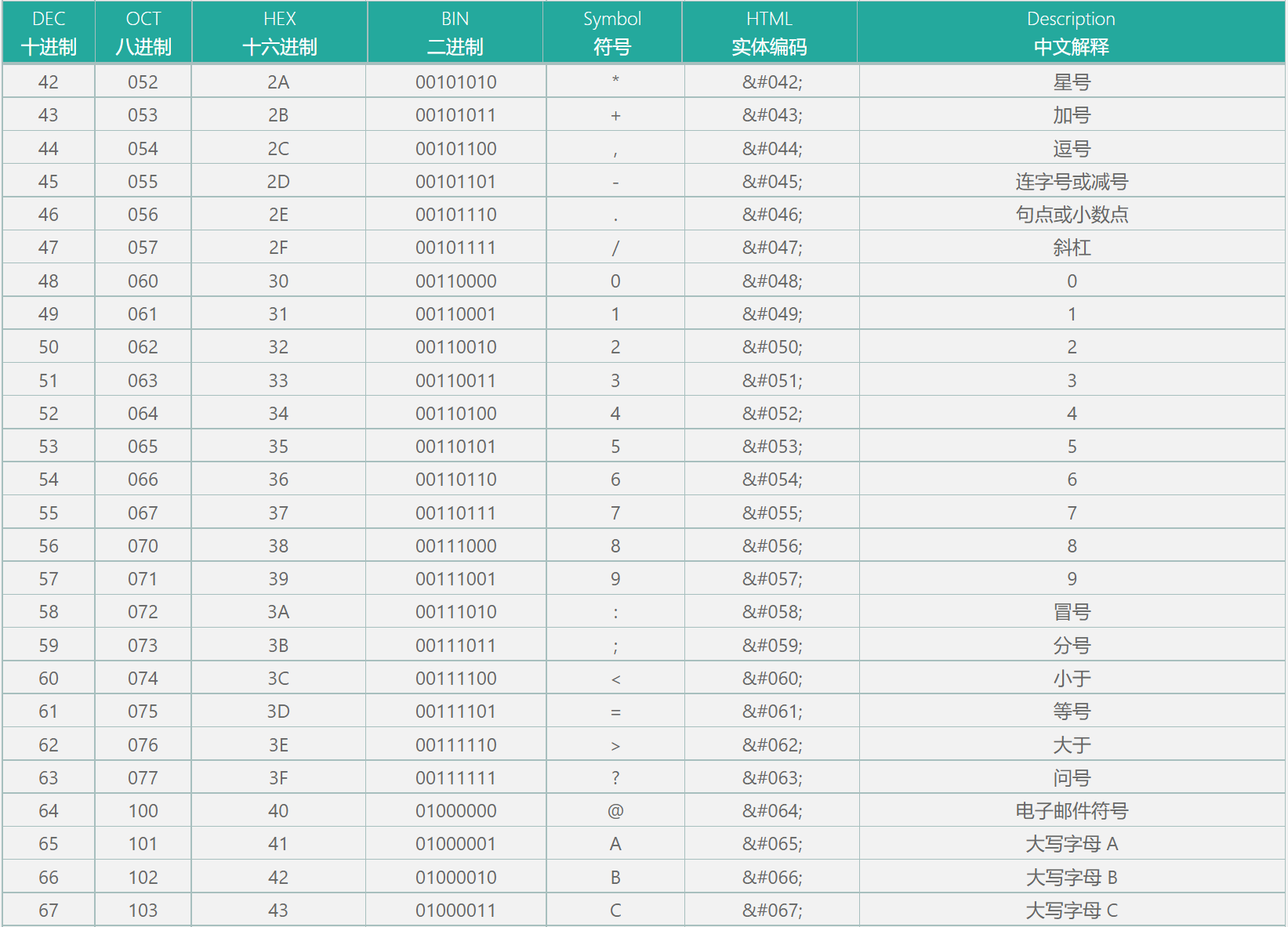
常用需要记的几个Ascii码如下
- 字符0-9的Ascii码: 48 - 57
- 大写字母A-Z的Ascii码: 65 - 90
- 小写字母a-z的Ascii码: 97 - 122(大小写a相差32)
- 空字符Ascii码: 0
- 制表符(tab)Ascii码: 9
- 换行符Ascii码: 10
其余为了统一文本的unicode-8之类的就不拓展了,总之二进制可以表示的除了数字文字还有包括各类文件等所有东西…
算数逻辑单元 ALU
ALU | Arithmetic and Logic Unit
ALU是计算机里负责运算的组件,基本由一个算术单元与一个逻辑单元组成,基本上是为了解决用逻辑门实现加法的单元
处理一位加法|半加器
一位加法(两个一位input)真值表如下
| InputA | InputB | Output |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 10 |
很明显除了第四行别的异或门都能处理,那么只要再异或门的输入ab上再加一个与门进行判断就能处理进位了
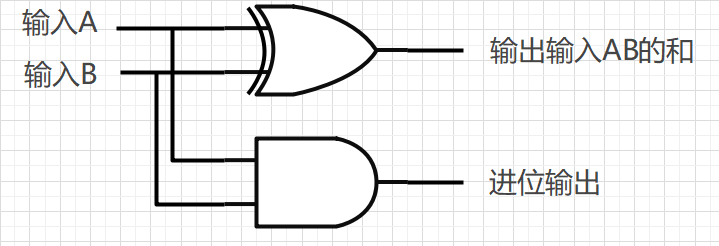
处理3bit加法|全加器
| InputA | InputB | InputC | 进位 | 总和 |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
全加器则是处理三位输入,除了ab还有进位输入c,然后将ab输入的输出和s与进位输入c输入到另一个半加器中即可输入abc的和,而该半加器的输出进位co与输入ab的输出进位co进行与操作后即可得到abc的进位co

八位行波进位加法器
将上一位全加器/半加器的进位输出作为下一位全加器的进位输入,依靠八个FA(Full Adder)或者一个HA(Half Adder)和七个FA组成
因为第一位没有进位输入所以可以使用HA